


In zijn Jubileumrede snijdt Geerten Meijsing het probleem van logische fouten in de Bob Evers-serie aan. Daarbij werpt hij onder andere de volgende vraag op:
Of de ontsnapping uit de kelder in San Francisco door gebruik te maken van de waterdruk (Hoog spel in Hong Kong): zou de druk van het water in de kelder niet groter worden dan de waterdruk die uit de kranen komt, zodat deze laatsten vanzelf ophouden te stromen?
Deze vraag hebben we voorgelegd aan Jan Prins, die onmiddelijk de ogen ten hemel sloeg en begon op te dreunen:
'Volgens de Britannica zijn drukken van 30 tot 100 pound per vierkante inch - dat is twee tot zeven kilogram per vierkante centimeter - gebruikelijk in waterleidingsystemen. Veertig tot vijftig pond per vierkante duim, oftewel twee-komma-acht tot drie-komma-vijf kilogram per vierkante centimeter, volstaat voor het leveren van een bevredigende waterdruk op de bovenverdiepingen van vier-hoge gebouwen. Voor brandbestrijding...'
'Hoho, wacht effe. Dus eh, als de leidingdruk daar in dat huis nou eens twee kilogram per vierkante centimeter was, om het laag te schatten...'
'Dan zou dat genoeg zijn om het water tot twintig meter hoogte op te pompen. Ga maar na: als je een kolom van tien meter water hebt met een doorsnede van één vierkante centimeter, dan is dat een totale hoeveelheid water van duizend kubieke centimeter oftewel één hele liter. En dat weegt precies een kilo. Geeft een kraan nou een druk van twee kilo per vierkante centimeter, dan kan-ie dus nog net optornen tegen een waterkolom van twee maal tien meter.'
'Hm. Maar het oppervlak van die kelder was 36 vierkante meter, als ik me goed herinner. Een kolom van tien meter weegt dan dus geen kilo, maar 360 ton. Waar blijf je dan met je kraantje van twee kilogram per vierkante centimeter?'
Jan werd nu merkbaar ongeduldig:
'Dat is toch duidelijk, sukkel! Als je de druk wilt bepalen die een vloeistofmassa op een horizontaal oppervlak levert, dan moet je het totale gewicht van die massa delen door dat oppervlak. Driehonderdzestig ton over zesendertig vierkante meter is 360.000 kilogram op 360.000 vierkante centimeter, en dat is dan weer precies één kilo per vierkante centimeter. Gesnapt?'
'Gesnopen. Het gaat dus niet om het totale gewicht van al dat water, maar om het gewicht per eenheid oppervlak?'
'Precies. Als die kelder twee keer zo groot was geweest...'
'Of twee keer zo klein...'
'Voor mijn part. Dan zou tien meter water twee keer zoveel of twee keer zo weinig wegen, maar de druk zou hetzelfde zijn, omdat dat gewicht verdeeld wordt over een oppervlak dat óók twee keer zo groot of klein is.'
'Hajuist. En hoe hoog stond het water ook alweer toen die deur het begaf?'
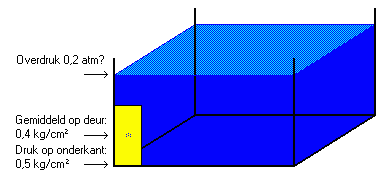
Jan dacht even na. 'Nou, zo'n dikke drie meter. De gemiddelde druk over de deur was dus ongeveer twee meter water, dat is twee ons per vierkante centimeter.'
'Dat lijkt ook niet veel.'
'Ja, maar vergeet niet dat dat in totaal drieduizend en zeshonderd kilo op de hele deur is. Dat zijn drie forse auto's. En dat hele gewicht wordt uiteindelijk opgevangen door de raakvlakken tussen de deur en de sponning: links en rechts twee meter, en negentig centimeter over de bovenzijde. Als die raakvlakken een centimeter breed zijn, dan spreken we over in totaal vierhonderdnegentig vierkante centimeter... en dus over een druk van ruim zeven kilogram per vierkante centimeter. Dat is aardig wat, hoor.'
'Toch niet genoeg, lijkt me. Ik weeg zeventig kilo. Als ik op een stoel ga staan met vrij dunne poten - laten we zeggen: met een gezamenlijk oppervlak van tien vierkante centimeter, dan drukken die poten ook met zeven kilogram per vierkante centimeter op de vloer. En ik moet de vloer nog zien die dát niet houdt. Er komt niet eens een afdruk in te staan, behalve als-ie van zachtboard is.'
'Hmm, daar zeg je wat... dat is inderdaad wel raar.'
'Zeg, Janneman... hoeveel hoger zou de druk worden als de luchtgaten dichtgemetseld waren?'
Jan trok een gezicht. 'Eens kijken: de kelder zou dan luchtdicht worden op het moment dat het water de bovenrand van de deur bereikte. Er staat dan zes meter lucht boven de deur. Die lucht heeft een druk van één atmosfeer, dat is grofweg één kilo per vierkante centimeter. Als het water een meter hoger stijgt, wordt de lucht samengeperst tot vijf zesde van zijn oorspronkelijke volume, dus de druk wordt zes vijfde keer zo groot: één komma twee atmosfeer. De gemiddelde druk over de deur is dan niet twee, maar vier ons per vierkante centimeter.'
'En over de raakvlakken?'
'Bijna vijftien kilo per vierkante centimeter.'
'Dat zijn jij en ik samen op een stoel met dunne poten. Nog steeds niet erg indrukwekkend, hè?'
'Ja, maar wacht eens even, zeg. Ik bedenk daarnet wat: dat stukje vloer waar een stoelpoot op drukt wordt aan alle zijden ondersteund door het omringende hout. Maar voor een willekeurige vierkante centimeter sponning waar die deur tegenaan drukt geldt dat niet. Ga maar na: aan de ene kant zit helemaal geen hout, want daar is het deurgat. Boven en onder loopt de sponning door. Die geeft geen extra steun, want daarop rust zelf óók weer vijftien kilo per vierkante centimeter. Alleen het hout aan de kant van de stijl helpt een beetje mee om de druk op te vangen. Maar uitgerekend in die richting ligt het grensvlak evenwijdig aan de nerf. En dat scheurt gegarandeerd uit hoor, neem dat nou maar van mij aan. Een stalen sponning zou het houden - maar een houten niet. Bovendien...' - Jan pauzeerde even.
'Bovendien wàt?'
'Bovendien stond er op de onderkant van de deur niet vier, maar vijf ons per vierkante centimeter. En -'
'Aangenomen dat de luchtgaten dichtgemetseld waren, dan altijd.'
'Aangenomen dat die dichtzaten, ja. En zou je nu misschien eens even je waffel willen houden en me laten rekenen? Fijn. Als we verder aannemen dat die negentig centimeter brede deur aan weerszijden één centimeter over de sponning heen stak, dan was onderaan de druk op de sponning vijfenveertig keer een halve kilo, is tweeëntwintig-en-een-halve kilo per vierkante centimeter sponning. Dus die stijl is natuurlijk van onder af opengescheurd.'
'Zeg, jongetje Prins?'
'Ja, wat is er NU nog?'
'Ik geloof dat ik het begin te snappen.'
'Och, rol om.'

Ook Frank Engelen heeft een beschouwing geschreven over deze kwestie: Druk met waterkracht. Gauw gaan lezen. Nee, laat maar, want die zultkop heeft zijn pagina's verloren laten gaan.

Terug naar de hoofdpagina van de "Duizend-en-enige hoofdstukken over Bob Evers"
Paginabaas:
Paul Vinkenoog <paul_op_vinkenoog_punt_nl>